trick for 1k raymarchers :: lighting
category: code [glöplog]
@psonice:
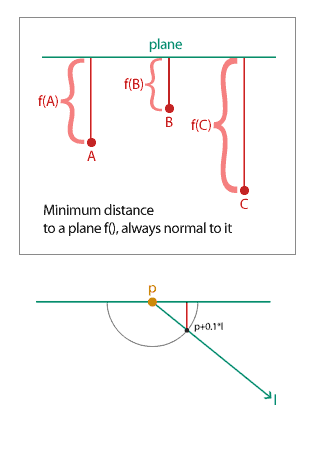
Well, suppose at p we have a plane instead of a curve surface (since the 0.1 or epsilon is little, we can suppose that).
p
____________________________
\
\
\ ray
So, the f() of the p+0.1*l will be maximum -- 0.1 -- when the ray is normal to that plane, and it will be less and less as the ray have less angle with the plane. The minimum distance to the plane to a point -- given by f() -- is always in a line normal to the plane and crossing the point.
Well, suppose at p we have a plane instead of a curve surface (since the 0.1 or epsilon is little, we can suppose that).
p
____________________________
\
\
\ ray
So, the f() of the p+0.1*l will be maximum -- 0.1 -- when the ray is normal to that plane, and it will be less and less as the ray have less angle with the plane. The minimum distance to the plane to a point -- given by f() -- is always in a line normal to the plane and crossing the point.
... Should I do an image of that?
I think I'm slowly starting to get it.. maths isn't my strong point, but I'll keep thinking it through until it makes sense. Thanks for the description + diagram, it's helping a lot (I've progressed from not getting how it can work at all without calculating the normal to nearly getting it completely.. just needs a final little gear to click into place!)
And you can improve the accuracy with:
Converges on the exact result of the dot product method as c -> infinity.
Code:
float d=f(p+0.1*l/c)*c;Converges on the exact result of the dot product method as c -> infinity.
Kinda sad that in reality this will "converge" to pure IEEE rounding artifact noise as c->infinity :D
Quote:
On my decent, 24 bit monitor the 2nd image looks better, very little visible banding.
Oh we're talking about the second image? Sorry, I have absolutely no banding on that one (MacBook Pro). I was comparing the banding in the first render to the non-banding in the second one. :)
The macbook pros use TN panels I think (or at least did), so you're possibly looking at a dithered 16bit image :)
The quality of the dithering seems to vary by a massive amount actually. On my cheap home screen it dithers by flickering the pixels between two shades, which looks really nasty in certain cases but works ok in others.
On my work box, I have a reasonable 20" imac screen which is TN/16bit, but I can't see any banding, flicker or dithering at all. It looks 24bit. I also have a reasonable quality HP screen, also TN, no banding or flicker here at least but if I look close I can see dithering. Both are massively better than my cheap screen at home :( (but probably cost a lot more!)
Btw, you can easily tell if you have a TN screen: set it to show a full screen of solid colour (grey works well). See if the top of the screen is the same colour as the bottom - TN screens look like you have a gradient. If you move your head up + down, the gradient moves. This makes them bad for graphics work ;)
The quality of the dithering seems to vary by a massive amount actually. On my cheap home screen it dithers by flickering the pixels between two shades, which looks really nasty in certain cases but works ok in others.
On my work box, I have a reasonable 20" imac screen which is TN/16bit, but I can't see any banding, flicker or dithering at all. It looks 24bit. I also have a reasonable quality HP screen, also TN, no banding or flicker here at least but if I look close I can see dithering. Both are massively better than my cheap screen at home :( (but probably cost a lot more!)
Btw, you can easily tell if you have a TN screen: set it to show a full screen of solid colour (grey works well). See if the top of the screen is the same colour as the bottom - TN screens look like you have a gradient. If you move your head up + down, the gradient moves. This makes them bad for graphics work ;)
kb: I was writing something along the lines of "up to the precision allowed by floats and f()", but then I figured you'd all be clever enough to see it was implied. ;)
Quote:
If you move your head up + down, the gradient moves. This makes them bad for graphics work ;)
It makes them bad for everything. ;)
just use more coder color gradients, the eye can easily be tricked and won't see the monitor restrictions anymore.. ;)
I thought this topic was about a lighting trick, not color banding on shit lcd displays :)
Tell that to the guy who blamed his lcd display for the fact that one image had more banding than the other (on the FUCKING SAME SCREEN), I'd say :)
But yeah, the trick is neat. Most fun part is that I tried to find ways to make it fail and had to realize that the "original" implementation would fail in all of those cases, too. Unless of course if you uncomment the normalize() ;)
That's maybe the one drawback - you need to magically know the magnitude of the gradient of the distance function. Might suck for complex ones but then again this is about 1k programming.
But yeah, the trick is neat. Most fun part is that I tried to find ways to make it fail and had to realize that the "original" implementation would fail in all of those cases, too. Unless of course if you uncomment the normalize() ;)
That's maybe the one drawback - you need to magically know the magnitude of the gradient of the distance function. Might suck for complex ones but then again this is about 1k programming.
I magically know the magnitude of the gradient of all distance functions! ;)
The world may now!
Thanks for the trick :)
Thanks for the trick :)
if it's a distance function, you know the magnitude for sure :) If it's just some sort of potential function kb is right, you pretty much have to find the magic constant by trial and error. But who cares, it's 1k coding indeed.
thanks for sharing iq, indeed, nice trick, not only for size optimization but also for speed ;)
speed:
kusma: just imagine some effect that needs like 1-6 march-steps only for the most of geometry...having like 4-6 more calls can be very frustrating in these cases !
also iq at some point proved that most sphere-marchers (atleast) have an average of like 20 steps...so 1 additional call instead of 4-6 is a speedup that cant be ignored...the higher the resolution the more it helps in speed-issues !
kusma: just imagine some effect that needs like 1-6 march-steps only for the most of geometry...having like 4-6 more calls can be very frustrating in these cases !
also iq at some point proved that most sphere-marchers (atleast) have an average of like 20 steps...so 1 additional call instead of 4-6 is a speedup that cant be ignored...the higher the resolution the more it helps in speed-issues !
atleast should have applied to "sphere-marchers", didnt survive in pointing that out correctly...
dryhumping this dead thread to get some attention, can someone test the final of my 1k on an ATI card?
http://www.pouet.net/prod.php?which=55469
http://www.pouet.net/prod.php?which=55469
Worked on my ATI 4850 here.
Still not movement here, ati 3870 - just a nice still picture in yellowish colors :)
*facepalm*
I updated my gfx drivers from 10.2 to 10.7 and it runs smoothly now - in blue colors :) ...dindn't know my drivers where THAT outdated - my bad :)
still picture still :(
