Interpolation in adaptive sub-sampling?
category: general [glöplog]
Decipher: it can hardly be a more waste of time than having to deal with the temporary obstacles presented to you by today's gpu-apis. Right now, to make a realtime demo, sure you should use hardware rendering. But there are certainly other arenas now and in the future where cpu-like thinking is valuable.
Besides, it must be fun doing some cpu-rendering, no?
Besides, it must be fun doing some cpu-rendering, no?
The basic principle is: if you subdivide on one side of the edge, you should also subdivide on the other side.
Let's say you have 32x32 square and want to go down a level. You trace extra 5 points (center and points on the edges) and subdivide to 4 squares sized 16x16. In the process, you have added 4 points on the edges, which affect neighboring 32x32 squares (unless they were already subdivided, but let's assume they were not). In this case, neighboring 32x32 squares also have to be subdivided, but you don't add extra 4 "black" points for them (center + 3 remaining edges), but instead subdivide them with "green" points. The "green" points don't cause further subdividions of their neighbors (but green points can be later replaced with "black" ones).
Of course there is a lot of room for optimization, but it's probably most simplified version of the algorithm.
Let's say you have 32x32 square and want to go down a level. You trace extra 5 points (center and points on the edges) and subdivide to 4 squares sized 16x16. In the process, you have added 4 points on the edges, which affect neighboring 32x32 squares (unless they were already subdivided, but let's assume they were not). In this case, neighboring 32x32 squares also have to be subdivided, but you don't add extra 4 "black" points for them (center + 3 remaining edges), but instead subdivide them with "green" points. The "green" points don't cause further subdividions of their neighbors (but green points can be later replaced with "black" ones).
Of course there is a lot of room for optimization, but it's probably most simplified version of the algorithm.
The waybackmachine is your friend :)
http://web.archive.org/web/20050328034750/home.tiscali.be/slinline/toc2.html
http://web.archive.org/web/20050328034750/home.tiscali.be/slinline/toc2.html
I was replying to rydis quest for the Trezebees II article.
KK: yes, i will try something like that i think.
datsua: thanks, ill take a look at it.
datsua: thanks, ill take a look at it.
Isn't the level 0 squares simply too large on the previous page pictures ?
krabob: with an overlay filter it doesnt seem so. if i understand what you mean.
Well, Decipher has a point ;) But I also like sw rendering even if it does not make sense;) Whatever technique you use, the problem with the highlights is the one in my drawing. Texture/highlight/whatever properties won't match up on the two sides of an edge. This is not related to software or hardware rendering - nor can you solve this with trilinear or any higher order interpolation. In h7 this was nicely concealed by brilliant texture art. This works for 8x8 to 1x1, but not for 32x32 to 1x1. However, you can actually avoid the problem by interpolating properly on the non-subdivided side, too. I drew triangles to describe this, but you don't need hardware rendering nor triangles. To do this in sw with axis-aligned rects: in my pic, you subdivide the right tall rect into two squares, but you pick the right middle pixel by interpolation and not by sampling. This will make the squares match with the next rect on the right side. (hope it's possible to get what i say without another drawing.)
One more point, with 32x32 it's easy to miss objects if they are too small. So you need to force subdivision around object centres if the object has 0 hits on the 32x32 grid but it is inside the view frustum...
One more point, with 32x32 it's easy to miss objects if they are too small. So you need to force subdivision around object centres if the object has 0 hits on the 32x32 grid but it is inside the view frustum...
Ger:
yes, i understand what you mean. maybe i need to find a way to go around the recursive-function i use, because its restricted. it recurses linearly on screensize which means some edges are not traced if i want to interpolate bigger with smaller blocks. may be an indexing issue aswell.
I have an own variable called blockSize which i can change from smaller to higher pow2 numbers. if i dont hit an object it does not matter that much right now. i have to take care of that later.
yes, i understand what you mean. maybe i need to find a way to go around the recursive-function i use, because its restricted. it recurses linearly on screensize which means some edges are not traced if i want to interpolate bigger with smaller blocks. may be an indexing issue aswell.
I have an own variable called blockSize which i can change from smaller to higher pow2 numbers. if i dont hit an object it does not matter that much right now. i have to take care of that later.
Also, I think I'm saying something similar to KK, but you don't want to sample but just interpolate at KK's "green" points to get things right. If you do sample, then you avoid one edge mismatch by creating three edge mismatches around the neighboring square...
Quote:
the problem with the highlights is the one in my drawing
but if there's such a blatant difference in lighting, how come the other square isn't subdivided? it should be way over the threshold.
Gargaj: I think he doesn't consider lighting for subdivision decisions, and he probably won't need to if he gets the tesselation right... 16x16 to 1x1 may look nice that way if I remember well. (maybe not 32x32...)
Btw. there may be no the blatant difference if you only look at the corners. See the right edge on this pic...
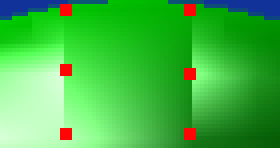
However, using the vertices in the middle of the left/right edge could make even this square look much better (it would get the highlight).
Btw. there may be no the blatant difference if you only look at the corners. See the right edge on this pic...

However, using the vertices in the middle of the left/right edge could make even this square look much better (it would get the highlight).
Yes. In that case he should detect that there's a large difference at the right vertical edge between the interpolated result of the middle square and the raytraced result from the right square. Since the rightmost square has to be subdivided (as it overlaps the horizon of the sphere), you need to either subdivide the square next to it as well, OR discard the raytraced colour on that centre vertex and use the interpolated result instead. The latter would be preferable since, if subdivision is based on colour difference along the edges (the way I suggested), then T-sections like that would only appear where there isn't much need for subdivision anyway, i.e. the raytraced colour for that point and the interpolated result from the neighbouring square are going to be close anyway.
Ger: about the picture - not if you look at the colors, but the sign of at least one component of the specular normal flips around, which should be considered...
i've implemented a threshold now, but it doesnt seem to be correct. its the power of the dot-products
i got some interesting results though:

if you look closely you can actually see the highlights. im not sure whats causing it to be white though. it may be because i sample on each point or something.
Code:
float threshold = 0.000001;
if ((dc[0] * dc[1] * dc[2] * dc[3]) > threshold)
i got some interesting results though:

if you look closely you can actually see the highlights. im not sure whats causing it to be white though. it may be because i sample on each point or something.
I would hereby like to welcome Pouet to the last 10 years of #scene.no on EFNet. :)
rydi: are you making this?
If not, you should. You should also not use the sqrt function, the squared length should also make the trick and be faster.
Code:
float length(vec3 a) { return sqrt(a.r + a.b + a.z); }
//...
float threshold = 0.000001;
if (abs(length(left)-length(right)) > threshold)
If not, you should. You should also not use the sqrt function, the squared length should also make the trick and be faster.
wtf? I meant this:
Code:
float length(vec3 a) { return sqrt(a.r + a.g + a.b); }
gloom \o/
xTr1m:
i was not actually trying that. i was using the dot-products from the four corners. i may have it wrong. im just trying out different things. that code may come in handy though.
i was not actually trying that. i was using the dot-products from the four corners. i may have it wrong. im just trying out different things. that code may come in handy though.
subdivision finally works! some artifacts but those are just a minor bug!

looks like threshold is the only thing to work on before getting everything perfect. :)

looks like threshold is the only thing to work on before getting everything perfect. :)
Ger: Interpolating "green" points was exactly what I had in mind.
rydi: For me it looks like you still have some subdivision issues - there should be no visible hard subdivision edge near specular reflection (this 32x32 square 1/2 radius above sphere center). Also it will be good idea to always subdivide if the shadowed/unshadowed status of corners don't match (this way you'll get non-blocky shadow edge).
Still, it's starting to look like proper raytraced sphere, so keep up the good work. :)
rydi: For me it looks like you still have some subdivision issues - there should be no visible hard subdivision edge near specular reflection (this 32x32 square 1/2 radius above sphere center). Also it will be good idea to always subdivide if the shadowed/unshadowed status of corners don't match (this way you'll get non-blocky shadow edge).
Still, it's starting to look like proper raytraced sphere, so keep up the good work. :)
ridy: maybe this also (in pseudo pseudo-code):
but maybe the sum of the delta's squares compared against the squared threshold is a more performing choice (less conditional statements...).
check also here: http://mrl.nyu.edu/~perlin/ghost/
Code:
if( abs(delta_R) > threshold ) return has_edge;
if( abs(delta_G) > threshold ) return has_edge;
if( abs(delta_b) > threshold ) return has_edge;
return has_not_edge;but maybe the sum of the delta's squares compared against the squared threshold is a more performing choice (less conditional statements...).
check also here: http://mrl.nyu.edu/~perlin/ghost/
i removed the middle points because it didnt work or i didnt manage to do it properly. however i used the same recursive function to recurse where uv coords didnt have flags and highlights. i am a little fed up with coding or i use time on the wrong things rather than the right ones. however i learn alot in the process. so it might take some time until i get the most optimal way. the code is so messy that changing a little thing might ruin it all or might take some time to update the rest.

as you can see in the picture theres something wrong because the subdivision doesnt do it at the edges of the shadows but outside.
in the picture the white dots are where there are no texture (no uv-flags that is true). the green dots are where all the corner edges have an uv-flag that is true. and the red ones should be where there are atleast more than one that is true or none of them are all true (but i think i have done something wrong in the algo that dont do this properly. i will check that later).
Code:
float w = dc[0] + dc[1] + dc[2] + dc[3];
if (w > powf(threshold, 0.009*keyFactor))
i dont know why i do it like this. i will change it later. but now there are so many things to work on. and the trace-code is 155 lines long :( so i have to do some cleanup.
Just release it like this and call it art!
