Math stupid question on continuous curve
category: general [glöplog]
WTF ?
http://www.iquilezles.org/apps/graphtoy/
Ok I'm 35 and my few math skills are lost in space, but:
On Iq's toygraph site, I'm quite fascinated by f(x)=sin(4*x)/x.
How a function with 1/x can "look" continuous for 0 ?
It is not continuous right ? ...but you can zoom in the top of the curve with iq's interface ... and it really looks continuous !!!
- Someone with fresher brain got a smart answer to this ?
- Do you know other simple equations with 1/x that avoid "discontinuity" ?
http://www.iquilezles.org/apps/graphtoy/
Ok I'm 35 and my few math skills are lost in space, but:
On Iq's toygraph site, I'm quite fascinated by f(x)=sin(4*x)/x.
How a function with 1/x can "look" continuous for 0 ?
It is not continuous right ? ...but you can zoom in the top of the curve with iq's interface ... and it really looks continuous !!!
- Someone with fresher brain got a smart answer to this ?
- Do you know other simple equations with 1/x that avoid "discontinuity" ?
well, a tiny amount either side of zero and it heads towards 4. At zero, you get a div0 error so I guess that result is thrown away (or a tiny number is added to zero). Otherwise, yes, if you zoom in an infinite amount you'll see a gap for sure. Keep zooming in :)
That explain the continuous look, and only that. (it should be discontinuous on 0)
Quote:
How a function with 1/x can "look" continuous for 0 ?
Take f(x) = x / x. When stated like that, it's 1 everywhere except at 0, where it's undefined. If you simplify it to 1, you get a function that's well-defined everywhere.
Same case with sinc. The expression sin(x)/x is undefined at x=0, but the 'patched' function "f(x) = sin(x)/x if x!=0, 1 if x=0" is defined over the real line and continuous everywhere. Furthermore, lim x->0 sin(x)/x=1. Note that neither the original nor the patched function have any discontinuities! Both are continuous over their whole domain; it's just that the expression sin(x)/x is undefined for x=0. When you have a single-point "hole" in the domain of a function for which a limit exists, it's called a "removable" or "cosmetic" singularity - you can easily define a modified function that agrees with the original function everywhere and includes the undefined point in its domain. The "x/x" I mentioned earlier is a trivial example of this. It's customary to present such functions with the easiest algebraic equation that defines them almost everywhere (in this case meaning, everywhere except for at most a countable number of removable singularities) and insert the necessary limits as necessary. Just take it as a somewhat sloppy but generally accepted shorthand.
A straightforward analytical way to see that lim x->0 sin(x) / x = 1 is to just plug it into the analytical definition of sin.
Code:
sin(x) = sum(k=0;inf) (-1)^k x^(2k+1) / (2k+1)!
=> sin(x)/x = sum(k=0;inf) (-1)^k x^(2k) / (2k+1)!
= 1 - (x^2)/3! + (x^4)/5! - (x^6)/7! + ...which is a power series that is both well-defined and convergent for x=0 and evaluates to 1 there (as should be obvious from the series expansion).
thanks for the interesting explainations twinside & ryg, I have to remember some stuffs about limits I guess...
It's called a removable singularity.
Quote:
A straightforward analytical way to see that lim x->0 sin(x) / x = 1 is to just plug it into the analytical definition of sin.
Series sucks, go French and use L'Hopital
ah ja, hospitalsreglen
Yes, mr.Hospital is what I thought when first seeing this function. But I haven't thought this before: it makes sense mathematically but it bugs me now how would you evaluate this on code? (it would divide zero by zero if you just replace x by zero). Gotta read the explanations cause they are interesting (and different ways to look at it than L'Hopital).
Ok, I see. You just discard the case where it's exactly zero. When it's very very close to zero, you get a sin(x) that is very similar to x, so dividing the two gets one. There is no really anything to plot at exact zero even if you would make the graph plot looks continuous near zero.
krabob, GraphToy discards infinites and NaNs by not drawing anything. Thing is you will hardly ever get an exact x=0 anyway (for the sin(4x)/x I mean), you must be really unlucky for a pixel to perfectly match x=0.
Even if it did, since x=0 is a removable singularity (limit in the left = limit in the right) only one pixel would be empty in the graph. Now, GraphToy draw lines with a width of 1.5 pixels, so the curve in the left and the curve in the right will account for the 0.5+0.5 = 1 pixel missing effectively filling the removable hole.
btw, at school we learned to solve the 0/0 cases by L'Hopital indeed, is not like that everywhere else, or are the countries renaming again the theorems for (old) political reasons?
Even if it did, since x=0 is a removable singularity (limit in the left = limit in the right) only one pixel would be empty in the graph. Now, GraphToy draw lines with a width of 1.5 pixels, so the curve in the left and the curve in the right will account for the 0.5+0.5 = 1 pixel missing effectively filling the removable hole.
btw, at school we learned to solve the 0/0 cases by L'Hopital indeed, is not like that everywhere else, or are the countries renaming again the theorems for (old) political reasons?
You can not use L'Hopital's rule, because the evaluation of the derivative of sin(x) uses the limit sin(x)/x as x->0. Circular proof.
i dont know iq release that stuff. clean interface, do what is it supposed to be, rocks solid (like shadertoy...). thx iq
and oh yeah
i forgot :
i forgot :
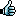
not sure, in fact it's a double limit: in two variables, isn't it?
lim(x->0, sin(x)/x) = lim( x->0, lim(y->0, sin(x+y)-sin(x)) / 1 ) and by exanding sin(x+y) in sinx*siny + cosx*cosy you get the same as directly appying L'Hopital lim(x->0, sin(x)/x) = lim( x->0, sin'(x) / x' )= lim(x->0,cos(x)/1) = 1/1 = 1
lim(x->0, sin(x)/x) = lim( x->0, lim(y->0, sin(x+y)-sin(x)) / 1 ) and by exanding sin(x+y) in sinx*siny + cosx*cosy you get the same as directly appying L'Hopital lim(x->0, sin(x)/x) = lim( x->0, sin'(x) / x' )= lim(x->0,cos(x)/1) = 1/1 = 1
I used the series expansion since you actually see what's going on, L'Hopital is easier to do mechanically but offers no insight. Not what I'm going for in an explanation :)
very true
btw, that's how Wikipedia has chosen to exemplify what a removable singularity is (with the very same sin(z)/z ). link me beautiful
imbusy, that would be a problem if using sin(x)/x -> 0 was the only way to determine that sin' = cos, but it's not. For example, you can compute the derivative of sin by formally differentiating its power series, which turns into the power series for cos, establishing the identity both algebraically and analytically. You can use sin(x) = im(exp(ix)) = (exp(ix) - exp(-ix)) / 2i which implies sin'(x) = (i exp(ix) - (-i) exp(-ix)) / 2i = (exp(ix) + exp(-ix)) / 2 = re(exp(ix)) = cos(x) - I really like this one. And there's definitely tons of other ways.
Awesome, had this in grade 10 or something.


This thread is now the random limit thread.
ryg, right. Depends on the way you define sin and cos.
I love pouët. Thanks so much for remembering me these math things :D
