Interesting graphic effect (morphing based on voxels)
category: code [glöplog]
The website https://www.okta.com/ features an interesting graphic effect. Does anybody know how it is done?
Yes, yes we do.
And it ain't voxels.
This appears to be bleeding-edge schmixel rendering.
This appears to be bleeding-edge schmixel rendering.
This thread made me discover the live version of Goxel so that's cool.
Basically I think I understand how it works. The models are 3D, the voxel coordinates (to me it seems to be voxels) are converted to 2D and while the model is being rotated, the voxels stay at the same place if they have reached the 2D coordinates where a pixel should be set in the target model.
Watching single pixels (they are just growing/shrinking squares, like used by p01 and others in tiny JS intros), they seem to fade from 3d rotation to a 2d linear movement during the latter part of a transformation, while they also adapt to their final size (or visibility) at the end. The final 2D coordinates seem to define the mapping to the closest rotated points at some timestep during the rotation.
Just my guess.
Just my guess.
Hilariously, it's a video.
@Gargaj: You're right. It's this one: https://www-assets.okta.com/homepage/a1_r06_v16_transp_cropped_mov_1M_crf63_1024px.webm
OK, next question: How did they calculate what's shown in the video? ;)
OK, next question: How did they calculate what's shown in the video? ;)
No idea, but similar thing could be done by for example:
1. create grayscale image
2. convert grayscale to pixel size
3. use pixel size as vertex z coordinate
4. to morph, rotate 90' and lerp between vertices
5. fudge until it looks decent
1. create grayscale image
2. convert grayscale to pixel size
3. use pixel size as vertex z coordinate
4. to morph, rotate 90' and lerp between vertices
5. fudge until it looks decent
https://tympanus.net/codrops/2019/01/17/interactive-particles-with-three-js/
or copypaste this code like "web designers" do :P
or copypaste this code like "web designers" do :P
Quote:
Yes, yes we do.
Wins.
oh, and Adok, it was done before:
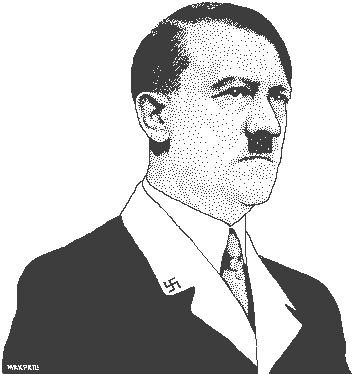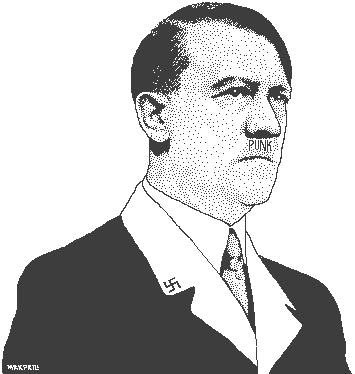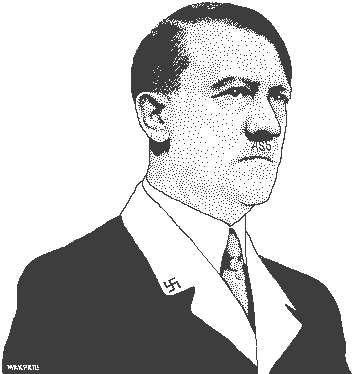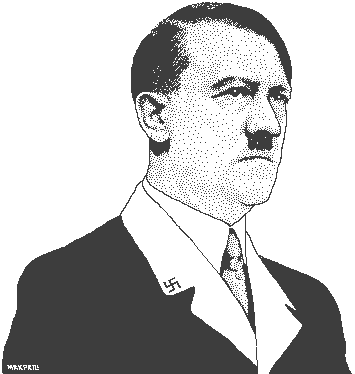
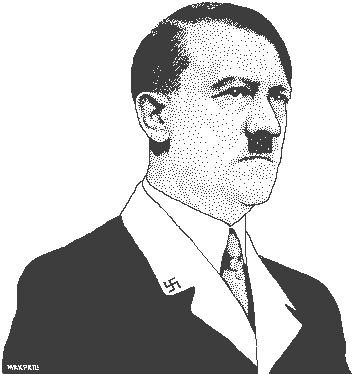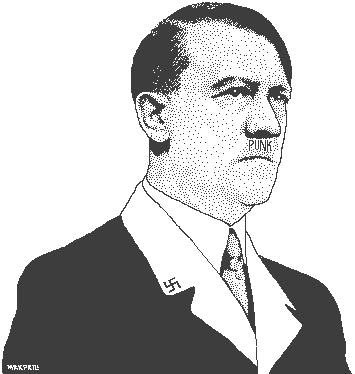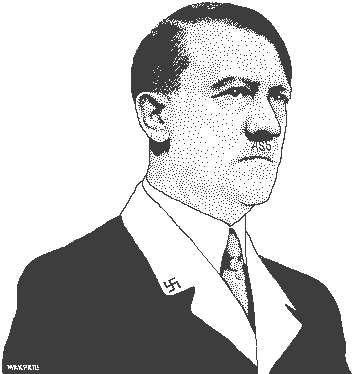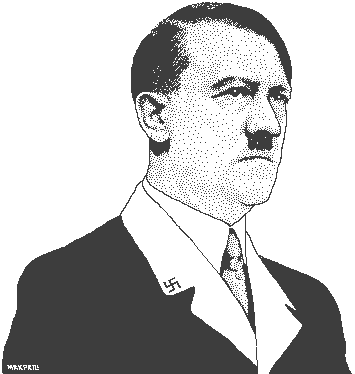
It might be as simple as a rotation on the y-axis and linear interpolation of points on the x-axis. Prolly every other face is opposite to one another (i.e. mirrored) on the y-axis.
hint: input photos are alternately lit from left and right, and the pixel size is the inverse brightness. sort it out :)
